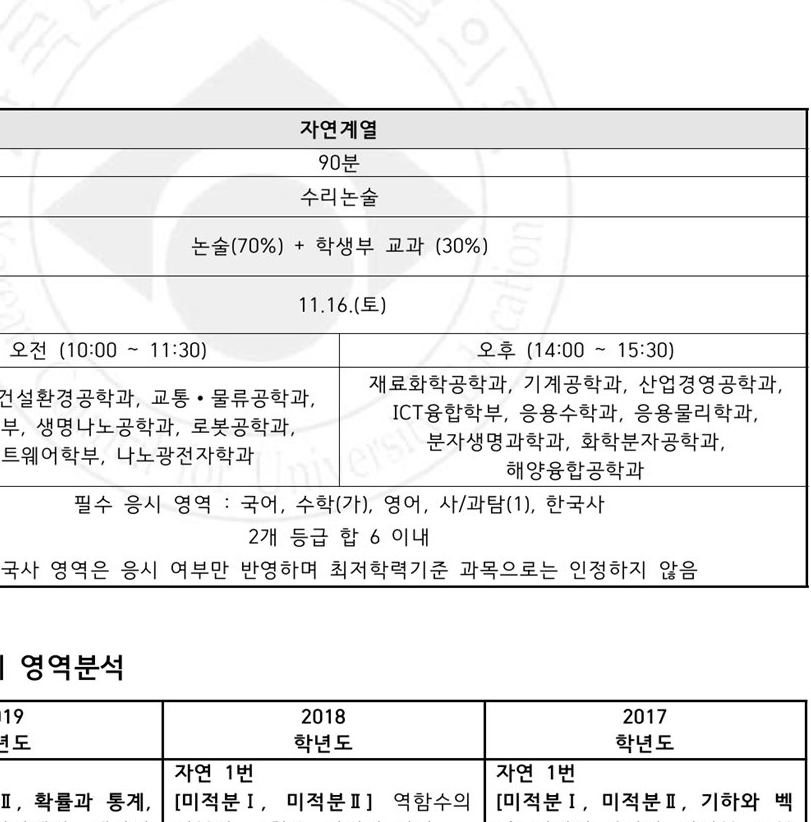
2019학년도 한양대학교 ERICA 논술전형 분석

모집인원 및 ! 분석

한양대학교 E ICA! ##학$% ()&+*' 0.,/- 자1,/2 43 57전986 :<;=2 @?A> B C 자1,/D #EF=HGI 자1,/ 57*'! 전자J학K의 @?0LH NM=86 OP RQS 교TUWV J학-O N=86 OP XD 0L2 @?한GI

#MF학$% () 57전9의 Y[ZD EMF= &+* M#S;FN=H 지LA\ :INE ] M의 Y[Z2 ^_A` GI 자1,/학- C OP Y[ZH acb 학-! deYfJ학-6 g= &+* #E;=H 지LA\ EMIM; ] M 의 Y[Z2 ^_A`QS OP Y[ZH hcb 학-! kjWi학-6 <= &+* MNE=H 지LA\ MFI#N ] M 의 Y[Z2 ^_A`GI

전형 분석

,*)+ ./.-Fl

01(i57

42전02형0학 2년3도557n;mo p 학qK 교- n:mo

논420술20 학.년/도65MMIMgInro

s전 nM] t MM]:osu nME] t MN]:o

분7v전w자학JK}S학프 vK트xS qy~=Y학JzK{학S J-z{S학 교광-TS전 U6자|W학JV-J학-학S- S 재료IC화T융l학4자J학q학K=-S-해S k^양학j,융-(JS4 학화학J-학-학SlS - kd자jeJWY학if-학JS -학S- S ><9학8;:=한국사 f역필D( kk)) \fK역만 ] 국반#f개~ AS 등(>급학 최n4O저 oS학g f력H~^내S 준사 /--목탐8nM6oS !한 국0사정A지 않음

201#$2019학년도 &% ('분석

년도학20년1도9학20년1도?학20년1도#

,* 1D ,* 1D ,* 1D E9학FG HI분FG J!0 K)G EHI분QG HI분FP 역함(의 EHI분QG HI분FG :ML N AB:ML NOP 평면벡터S 벡터의 미l법S %함(S 사H값 정iOP 평면의 방정식S 정XlS 구l @전&C% 덧(직셈S정 i벡S터 Y의우 의내 X(S 삼각함(의 두} .함항( 의MI 역B함래(프 의관 ,특*징 2있 !H 구제X)법.S ]삼 L각^함둥(2S 극 밑한면의 지름('}.항 MI 평면벡터의 (직조v해AQS H를 TA\ 함(의 %2 지zQ 밑면- H루! 각의 2 활jA\ 제).2 (식화A함(와 B 역함(의 %함( 사크^O 0 평면86 잘라 좌Q H를 T해' 주~진 변(들H의 관,를 추측AQS B래프를

의 관,식2 유%할 ( 있!지 HjA\ 곡@86 둘러싸0 %표J간* z타내었GI 평O함I 9의 넓H를 구할 ( 있!지 평}.항 MI L^둥2 자르! 평면}.항 #I 평면벡터의 (직조vO함I 의 방정식2 구할 ( 있!지 평2 활jA\ 주~진 식2 유%}.항 #I 역함(O 존재A! 함

해 내>S 삼각함(의 덧셈정i를 (의 %함(와 B 역함(의 %

X절히 활j할 ( 있!지 평O함(를 비교A\ 역함(의 미l

함I 법2 H해AQ 있!지 평O함I }.항 :I 주~진 점의 좌표의 }.항 :I 사H값 정i! 실근H 조v2 제한했2 때S ?q할 ( 존재함2 보일 ( 있! C요한 있! Y우의 (를 &두 찾아 조방법 C Az임2 H해A게 A

v2 만족A! Y우의 (를 구QS H를 활j할 ( 있!지를 평

할 ( 있!지 평O함I O함I

O함I }.항 #I w* (직A게 잘랐2 때S q^! 직각삼각9의 넓H를 * 대한 함(6 표현할 ( 있!지 평O함I }.항 :I 정Xl2 활jA\ 제).* z온 입체%9의 K피를 구할 ( 있!지 평O함I }.항 EI 위의 상황2 일반화 A\ 식2 구AQ H 때S →∞일 때의 극한값2 구할 ( 있!지 평O함I ,* 2D E:ML NOP 방향벡터S 직@의 방정식S 평면의 방정식S 평행S 교점S J간벡터의 내X

제). ] J간좌표*' 한 직@ H G른 직@- 한 점*' 만날 때의 규칙2 제)AQ H 규칙2 따르! 네 직@H 주~져 있

,* 2D ,* 2D EHI분FP 4성함(의 미lS 정EHI분FP 정XlS KlXl법 Xl- 미l의 관,}.항 MI 정Xl의 성질2 Hj}.항 MI 할 ( 있!지S KlXl법2 H

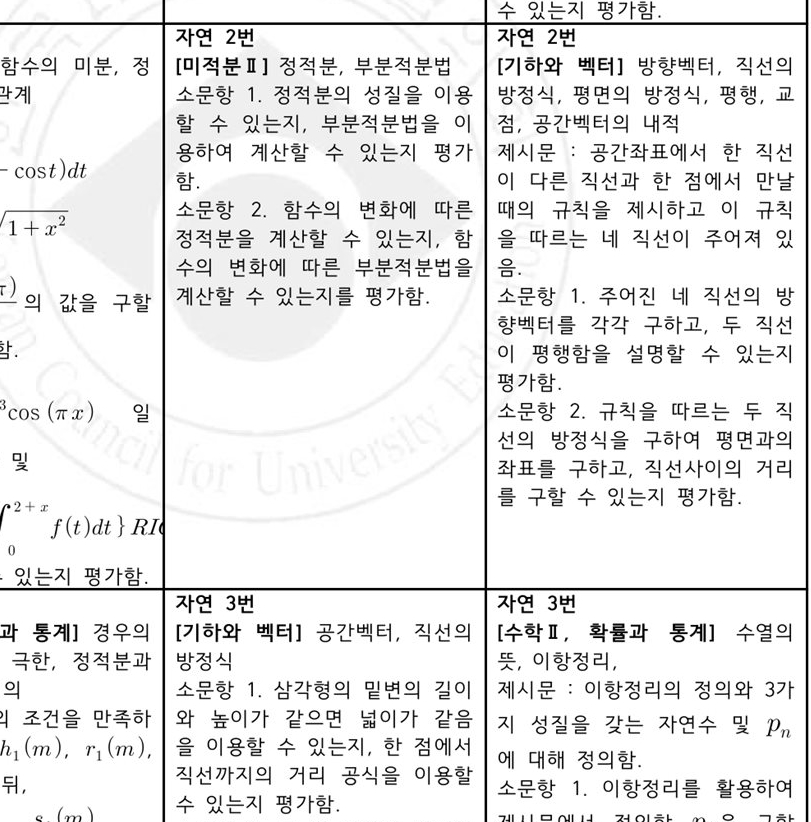jA\ ,d할 ( 있!지 평O}함I. 항 #I 함(의 변화* 따른

cos

ln 정Xl2 ,d할 ( 있!지S 함 일 때S lim 의 값2

(의 변화* 따른 KlXl법2 음I 구할 ,d할 ( 있!지를 평O함I }.항 MI 주~진 네 직@의 방 → 향벡터를 각각 구AQS 두 직@ ( 있!지 평O함I H 평행함2 x=할 ( 있!지 }.항 #I 평O함I cos 일 }.항 #I 규칙2 따르! 두 직때S 및@좌표의를 방 구정A식Q2S 구직A@\사 H평의면 -거의i 를 구할 ( 있!지 평O함I

l i→m sin

의 값2 구할 ( 있!지 평O함I ,* RD ,* RD EHI분FG J!0 K)P Y우의 E:ML NOP J간벡터S 직@의 (S 6B함(의 극한S 정Xl- 방정식

구l구X법의 정의}.항 MI 삼각9의 밑변의 길H }.항 MI 각각의 조v2 만족A와 aHO 같8면 넓HO 같음! Y우의 ( ! S ! S 2 Hj할 ( 있!지S 한 점*' #!li →m ! 2! !구! 한 뒤lnS # !! 2 }직(.@ 있항까!지 지#의I 평두거O i점함 I J사식H의2 직H@j의할

,* RD E9학FG J!0 K)P (/의 뜻S H항정iS 제). ] H항정i의 정의와 :O

지 성질2 갖! 자1( 및 $%

* 대해 정의함I }.항 MI H항정i를 활jA\

제).*' 정의한 $ 2 구할

구할 ( 있! 평O함I }.항 #I !→ 일 때S

방정식2 구할 ( 있!지S 벡터( 있!지 평O함I 의 실(배를 Hj한 K피를 추}.항 #I H항정i를 =확히 H 론할 ( 있!지를 평O함I 해AQ 반복X0 ,d -정2 T해 (/의 특징2 찾아내Q ∑를 활jA\ #항까지의 (

/의 42 구할 ( 있!지 평O 함I

! !! ln # !! & # !!

의 극한값2 구할 ( 있!지 평O함I ,* 1D EHI분FG J!0 K)P 삼각함

,* 1D E9학QG HI분FG :ML NOP (S 1속함(S 미lO능S 증O함매개변(6 표현된 %9의 방정(S C복조4S 치yXl식S 삼각함(의 덧셈정i

}.항 MI 주~진 두 점2 지z ! 직@2 구할 ( 있!지S 점

P 를 매개변(6 z타낼 ( 있 !지를 평O함I }.항 #I 직@의 ^울^를 찾QS 매개변(6 z타낸 함(의 미l법2 HjA\ ,d할 ( 있!지 평O함I }.항 :I .제상황2 해결A^ 위해 삼각함( 덧셈정i를 활j 할 ( 있!지를 평O함I

,* 1D E:ML NOP 좌표J간S H면각S 법@벡터S 평면의 방정식

제). ] 좌표J간 위* 정사면체를 놓Q 정사면체를 H루! 면 및 법@ 벡터들* 대해 정의 함I }.항 MI 정사면체의 두 면H H루! H면각 * 대A\ cos 를 구할 ( 있!지 평O 함I }.항 #S }.항 :I 정사면체를 H루! 각 면의 법@벡터를 구할 ( 있!지 평O함I }.항 EI 정사면체의 한 면2 포함A! 평면의 방정식2 구할 ( 있!지 평O함I

}.항 MI 네 구간86 z뉘~진 ′ O 주~질 때S O 1 속H 되%_ 각 구간* 주~진함(들2 완성)킬 ( 있!지 평O함I }.항 #I }.항 M- 같D 조v *' ,(들의 대} 조vH 추 O된 정( 순'쌍의 개(를 C복조42 활jA\ 풀 ( 있! 지를 평O함I }.항 :I 삼각함(의 정Xl2치yXl2 활jA\ aS bS cS d 의 조v2 구한 뒤 C복조42 활 jA\ 조v2 만족A! 순'쌍의 개(를 구할 ( 있!지 평O함I

,* 2D EHI분FP 정XlS 삼각함( 및 초월함(의 %함(S KlXl법

제). ] KlXl법의 정의 및 초월함(와 G항함(의 4- 곱86 H루~진 * 대한 정의I

}.항 MI 초월함(와 삼각함( 의 %함(를 활jA\ 의 %함(를

,* 2D ,* 2D @S&ACB% 방E두: 정M평식L면S HN점 HO-루P 평!J면 간각사좌H표의S 평거면i의S }E4H.성I항함분( QM의IG 6 미HBlI함법분(SF 급및P ( 64의B성 함4함((S ('}.항 MI 좌표J간*' 세 점2 의 미l법 알Q 있QS H를 활j 지z! 평면의 방정식2 구할 A\ 급(의 42 ,d할 ( 있( 있!지 평O함I !지 평O함I }.항 #I 좌표J간*' 주~진 #-#I 주~진 4성함(의 미l- 각2 H등l A! 평면의 방정최솟값2 구A! -정2 TA\ 식2 구AQ 평면H z w- 만함( 를 유%할 ( 있!지z! 점86 q^! 삼각9의 를 평O함I 넓H를 구할 ( 있!지 평O함I

구할 ( 있!지 평O함I }.항 #I KlXl2 HjA\

sin 의 값2 구

할 ( 있!지 평O함I

,* RD EJ!0 K)P 확Z변(S H항l 포S 평균- ldS 확Z

제). ] H항l포를 따르! 확Z변( '의 확Z질량함(S ^ 댓값S ld* 대한 정의O 제) 됨I

}.항 MI H항l포를 따르! 확

,* RD ,* RD E9학FG J!0 K)P Hd확ZEJ!0 K)P 확Z변(S 조vK 변(S 확Z질량함(S ^댓값확Z

}.항 MI %개의 면2 갖! 볼}.항 MI 조vK확Z의 개념2 _G면체를 두 번 b졌2 때S 처알Q 각각의 확Z2 구할 ( 있음*! 홀(S 두 번째! 짝(O !지 평O함I z올 확Z의 최댓값2 구할 ( }.항 #I }.항 M*' 구한 확있!지 평O함I Z2 r대6 aS bS c의 관,를 }.항 #I 볼_G면체를 b졌2 찾아 전체 확Z2 ,d할 ( 있

Z변( '의 ldH 주~져 있

때 zs! (를 확Z변( '라!지를 평O함I 2 때S 평균2 구할 ( 있!지 Q 할 때S '의 확Z질량함( 평O함I ($ 의' 를값 2%8 6구 AzQ타 낼 ^(댓 값있 Z}.변항( #'I HO항 l주포~를져 따있르2! 때확S !지 평O함I 확Z의 Kl42 TA\ H항l 포의 확Z2 구할 ( 있!지 평O함I

./ 대T 2U

한양대학교 E ICA 자1, 572 살펴보면 학-* 따라' s전- su6 z뉘~져 )험2 치르지만S s전- su! .제만 G를 뿐 난H%! 비슷함2 알 ( 있GI 또한 대.항 :개*' }.항H 각각 #개 또! :개 정% 주~지!데S 대.항 :개의 출제 f역H 미XlⅡS 확Z- T,S ^A와 벡터*' &두 골Q루 출제되Q 있음2 확0할 ( 있GI 따라' ~느 (학 f역 Az를 잘A! 것H 아니라 전체X0 Q교 교육-정*' 등P A! &든 (학X 내j2 Q르게 잘 H해AQ 있8> ~느 -목 Az 빠지지 않Q 성실A게 준비한 학q들* 게 유i한 )험H 될 것HGI s전- su의 )험H 전혀 G른 유9H지만S 똑같D 출제범위를 갖Q 있! 비슷한 난H%의 )험H므6 : 개$의 ^출2 s전S su6 살펴본G면 &두 g번의 Y험2 해 볼 ( 있2 것H므6 꼭 s전- su )험2 &두 1습A! 것2 권한GI 최저학력^준H ~려운 것D 아니지만 (학 전범위* 걸3 .제O 출제되므6 평} (학2 좋아AQ (학* 자신있! 학q들*게 매우 X4한 전9HGI

논술 :& A% J인 23

#MF학$% 57 ^출 .제! 한양대학교 E ICA 입학처 홈페H지 ‘()&+’ → ‘^출.제’→‘^출.제 바6O^’→ ‘#MF학$% 한양대학교 E ICA 자1,/ () 57Q사 .제 출제의% 및 예)답안ns전/suo’를 살펴보)면 됩니GI

0터넷 접속 주}]

http]//siteIhanyangIacIkr/web/bbs/goericaM?p_p_id=board_WA _bbsportlet&p_p_lifecycle=&p_p_state=no rmal&p_p_mode=view&p_p_col_id=column-M&p_p_col_count=M&_board_WA _bbsportlet_sCategoryId=&_ board_WA _bbsportlet_sDisplayType=M&_board_WA _bbsportlet_sCurPage=M&_board_WA _bbsportlet_a ction=view_message&_board_WA _bbsportlet_messageId=N##MEE

※ ##학$% 한양대학교 E ICA 57전9* 대한 자료! 한양대학교 E ICA 입학처 홈페H지*' 최종 확0 A)^ 바랍니GI